FAQ - Frequently Asked Questions zur Theoretischen Informatik I
-
Warum gilt die Gleichung: 2ø={Ø}?
-
Mit welchen Methoden kann die Nicht-Regularität
von Sprachen bewiesen werden?
-
Warum ist L+=ø
für L = {epsilon}?
-
Wie lautet
die Churchsche These? Was folgt daraus?
-
Kann
eine nichtreguläre (weder links- noch rechtslineare) Grammatik eine
reguläre Sprache erzeugen?
-
Was
sind die Unterschiede und Gemeinsamkeiten zwischen rechts- und linkslinearen
Grammatiken?
-
Was ist Diagonalisierung?
-
Warum ist die Primzahlzwilling-Funktion
f: N->{0,1} berechenbar?
-
Kann
es verschiedenen minimale Automaten für ein Problem geben?
-
Was
bedeuten die Begriffe injektiv, surjektiv und bijektiv?
-
Gegen
welche Operationen sind reguläre Mengen abgeschlossen?
-
Wann ist eine Menge abzählbar?
-
Warum gilt für Sprachen
L1, L2, L3 die Beziehung (L1 . L2) . L3 = L1 .
(L2 . L3)?
-
Wann ist eine
Menge/ein Problem entscheidbar?
-
Sei
A ein endlicher Automat. Ist L(A) = Ø entscheidbar?
-
Wie beweise ich für zwei
Mengen A und B, daß A = B gilt?
-
Was ist eine partielle Funktion?
-
Warum
ist eine Menge von Wörtern, die mit der leeren Menge konkateniert
wird, die leere Menge?
-
Gibt es ein Verfahren zur eindeutigen Bestimmung, ob eine Sprache regulär
ist?
-
Ist
entscheidbar, ob die von einem endlichen Automaten akzeptierte Sprache
unendlich ist?
-
Was ist eine Grammatik?
-
Gibt
es Grammatiken die sowohl links- als auch rechtslinear ist?
-
Wie wird ein indirekter
Beweis durchgeführt?
-
Wieviele
endliche deterministische Automaten mit n Zuständen gibt es?
-
Was ist die Backus-Naur-Form?
-
Wann
stoppt ein endlicher deterministischer Akzeptor seine Berechnung?
-
Enthält
jede unendliche Sprache das leere Wort?
-
Ist jede
Teilmenge der Menge X* eine reguläre Sprache?
-
Wie
lautet (bezüglich der Inklusion) die kleinste und die größte
reguläre Sprache über X?
-
Was
ist eine totale Funktion und wie ensteht sie aus einer partiellen Funktion?
-
Was besagt der Satz von Rice?
-
Was sind Ableitungsbäume?
-
Warum
kann die in der Vorlesung vorgestellte abstrakte Maschine alle Funktionen,
auch nicht-berechenbare, in einem Schritt berechnen?
-
Ist
die Vereinigung zweier linkslinearer Sprachen wieder linkslinear?
-
Wie
kann man aus einem nichtdeterministischen endlichen Automaten A einen äquivalenten
deterministischen endlichen Automaten A' mit L(A)=L(A') konstruieren?
-
Was ist ein Palindrom?
-
Wie
beschreibt man einen deterministischen endlichen Akzeptor?
-
Was ist eine reguläre Sprache?
-
Was sind Epsilon-Übergänge?
-
Was bedeuten die Begriffe "Wort",
"Alphabet", "Sprache"?
-
Was besagt die Churchsche These?
-
Wie
bestimme ich zu einer rechtslinearen Grammatik in Normalform einen endlichen
Akzeptor?
-
Was ist ein regulärer Ausdruck?
-
Wieviele
Zustände hat ein minimaler deterministischer endlicher Automat (DFA)?
-
Ist
entscheidbar ob zwei endliche Automaten äquivalent sind, d.h. die
gleiche Sprache akzeptieren (sog. Äquivalenzproblem)?
-
Wann
heißen eine Grammatik G und eine Sprache L mehrdeutig?
-
Welche
Beschreibungsmöglichkeiten gibt es, um eine reguläre Sprache
zu definieren?
-
Wie
beschreibt man einen nicht-deterministischen endlichen Akzeptor?
-
Was ist die Chomsky-Hierarchie?
-
Wann sind zwei Grammatiken
äquivalent?
-
Was ist eine kontextsensitive
Grammatik?
-
Wann
akzeptiert ein endlicher, nichtdeterministischer, vollständiger Akzeptor
A ein Wort w aus L(A)?
-
Können
zwei verschiedene Grammatiken die gleiche Sprache erzeugen?
-
Wie
geht man vor, wenn man einen nichtdeterministischen Akzeptor mit Hilfe
einer imperativen Programmiersprache (z.B. C) implementieren möchte?
-
Was ist die Chomsky-Normalform?
-
Was sind rekursive Grammatiken?
-
Was ist ein Automatenmorphismus?
-
Welche Abschlusseigenschafen
hat DA?
-
Was ist das Selbstanwendungproblem?
-
Welche
Abschlußeigenschaften erfüllt die Klasse der kontextfreien Sprachen?
-
Woran erkennt
man eine kontextfreie Grammatik?
-
Was ist das Halteproblem?
-
Wieso
sind kontextfreie Sprachen nicht abgeschlossen gegen Durchschnittbildung?
-
Was sagt das "Wortproblem"
aus?
-
Fragen ohne Link wurden von Ihren Kommilitonen
gestellt. Dazu werden noch Antworten gesucht.
Warum gilt die
Gleichung: 2ø={Ø}?
Mit 2M bezeichnen wir die Potenzmenge der Menge M, also
die Menge aller Teilmengen von M. Ist nun M die leere Menge, so ist die
einzige Teilmenge der leeren Menge die leere Menge selbst. Folglich besteht
2ø nur aus dem Element Ø.
Mit welchen Methoden
kann die Nicht-Regularität von Sprachen bewiesen werden?
Mit Hilfe des PUMPING-LEMMA und des STRUKTUR-SATZES VON NERODE. Dabei
beschreibt das Pumping-Lemma nur eine notwendige Bedingung für reguläre
Sprachen, während der Struktursatz von Nerode außerdem noch
eine hinreichende Bedingung für reguläre Sprachen und eine Charakterisierung
der Zustandszahl minimaler Automaten enthält.
Warum ist L+=ø
für L = {epsilon}?
L+ ist definiert als L* ohne epsilon, also:ÊL+
= L*\{eps}. Für L={epsilon}: {epsilon}*={epsilon}; {epsilon}\epsilon=ø.
Wie
lautet die Churchsche These? Was folgt daraus?
Die Klasse der Turing-berechenbaren Funktionen stimmt mit der Klasse
der intuitiv berechenbaren Funktionen überein. Die Churchsche These
läßt sich nicht beweisen, da sie mit dem Begriff "intuitiv berechenbare
Funktion" einen formal nicht definierten Begriff benutzt. Für Fragen
der Berechenbarkeit ist die Wahl des Rechnermodells unerheblich, solange
es so viel kann wie Turingmaschinen.
Kann
eine nichtreguläre (weder links- noch rechtslineare) Grammatik eine
reguläre Sprache erzeugen?
Ja, auch wenn eine Grammatik nicht regulär (also weder rechts-
noch linkslinear) ist, kann die durch sie erzeugte Sprache regulär
sein. Die Regularität einer Grammatik ist also eine hinreichende Bedingung
für die Regulärität der von ihr erzeugten Sprache, aber
keine notwendige.
Was
sind die Unterschiede und Gemeinsamkeiten zwischen rechts- und linkslinearen
Grammatiken?
Gemeinsamkeiten: Beide Grammatiktypen erzeugen die Klasse der regulären
Sprachen, bei beiden wird jeweils nur ein Nonterminalsymbol abgeleitet,
und nach der Ableitung taucht auch bei beiden höchstens ein Nonterminalsymbol
auf.
Unterschied bei der Bildung der Regeln: Bei rechtslinearen Grammatiken
steht das Nonterminalsymbol (wenn eins vorhanden ist) nach der Ableitung
ganz rechts im Wort. Bei linkslinearen Grammatiken steht es ganz links.
Was ist Diagonalisierung?
Die Diagonalisierung, oder genauer, das Cantor'sche Diagonalisierungsverfahren
(Skript 2.2 Die Existenz nicht-berechenbarer Funktionen -> Satz E), stellt
eine indirekte Beweistechnik dar, die in der Informatik gerne und viel
benutzt wird, um die Nichtentscheidbarkeit von Problemen (oder Mengen)
nachzuweisen. Dazu wird eine (fiktive) Tabelle aller Möglichkeiten
erstellt, die dann mit Hilfe einer (geeignet definierten) Funktion zu einem
Widerspruch geführt wird. Die Diagonalisierung wird in einer von drei
Varianten verwendet, die sich von der Zielrichtung her etwas unterscheiden
und sehr gerne miteinander verwechselt werden.
-
Variante: dient dem Nachweis, daß eine gegebene Menge nicht rekursiv
ist,
-
Variante: zeigt, daß eine gegebene Menge nicht einmal rekursiv aufzählbar
ist,
-
Variante: zeigt, daß nicht alle Funktionen mit einer bestimmten Eigenschaft
Element einer als rekursiv aufzählbar bewiesenen Menge sind
Warum ist die
Funktion f: N -> {0,1} mit
 berechenbar?
berechenbar?
Eine Funktion ist genau dann berechenbar, wenn es einen Algorithmus
gibt, der für alle Werte aus dem Definitionsbereich terminiert und
den Funktionswert liefert.
Zwei Primzahlen mit dem "Abstand" 2 bilden einen Primzahlzwilling.
Beispiele: (3,5), (101, 103). Wieviele solcher Zwillinge existieren ist
noch nicht bekannt.
Tatsächlich ist die Anzahl der Primzahlzwillinge für die
Beantwortung dieser Frage nicht von Bedeutung. Offensichtlich hängt
der Funktionswert von f nicht von seinem Argument ab. Es sind zwei Fälle
zu unterscheiden: Entweder gibt es unendlich viele Primzahlzwillinge, oder
nur endlich viele. Für beide Fälle läßt sich ein Algorithmus
angeben: Die Konstante 1 oder die Konstante 0. Da einer der beiden Fälle
vorliegt, ist die Funktion berechenbar.
Nun könnte man einwenden, daß es Aufgabe der Funktion sei
herauszufinden, welcher der beiden Möglichkeiten der Fall ist. Ersetzt
man den Satz "falls es unendlich viele Primzahlzwillinge gibt" durch ein
nüchternes A (für eine wahre oder falsche Aussage) so wird die
Beantwortung dieser Frage intuitiver, obwohl sie sich nicht verändert
hat. Wahrscheinlich besteht die Tücke dieser Aufgabe darin, daß
sie im Umfeld von Automaten und anderen Methoden zur Formulierung von Algorithmen
gestellt wurde. Das führt dazu, daß bei jedem Problem an dessen
maschinelle Lösbarkeit (bzw. Entscheidbarkeit) gedacht wird, auch
wenn danach gar nicht gefragt war.
Kann
es verschiedene minimale endliche Akzeptoren für eine reguläre
Sprache geben?
Nein, nach dem Struktursatz von Nerode sind die minimalen Automaten
(bis auf Isomorphie) gleich. Jeder Zustand repräsentiert eine Äquivalenzklasse
der Nerode-Relation.
Was
bedeuten die Begriffe injektiv, surjektiv und bijektiv?
Sei f : X -> Y eine Abbildung, mit der Urbildmenge X und der Bildmenge
Y.
f ist surjektiv, wenn für alle Elemente y aus Y ein Element x
aus X existiert mit f(x) = y.
f ist injektiv, wenn für alle Elemente x1, x2 aus X gilt. f(x1)
= f(x2) => x1=x2.
f ist bijektiv, wenn f surjektiv und injektiv ist.
Gegen
welche Operationen sind reguläre Mengen abgeschlossen?
Die regulären Mengen sind abgeschlossen gegen Vereinigung, Kleenescher
Hüllenbildung (*-Bildung), Konkatenation und Durchschnittbildung.
Weiterhin ist die Klasse der regulären Mengen abgeschlossen gegen
Komplementbildung, Substitution mit regulären Sprachen, Homomorphismus
und inversem Homomorphismus sowie unter Quotientenbildung mit beliebigen
Mengen.
Wann ist eine Menge
abzählbar?
Eine Menge A heißt abzählbar, falls es eine bijektive Funktion
f : N -> A gibt oder - was gleichbedeutend ist - falls es eine bijektive
Funktion f : A -> N gibt.
Warum gilt für
Sprachen L1, L2, L3 die Beziehung (L1 . L2) . L3
= L1 . (L2 . L3)?
Die Konkatenation . ist eine assoziative Operation.
Wann
ist eine Menge/ein Problem entscheidbar?
Sei X eine Menge. Eine Teilmenge M heißt entscheidbar, wenn es
einen Algorithmus gibt, der für beliebiges x aus X feststellt, ob
x zu M gehört oder nicht. Der Algorithmus liefert also nur die Antworten
"ja" (meint x in M) oder "nein" (meint x nicht in M).
Wenn man von entscheidbaren Problemen spricht, so wandelt man das Problem
zunächst so um, daß eine Menge entsteht, die alle positiven
Fragestellungen des Problems enthält, also die Fragestellungen, bei
denen der Algorithmus "ja" liefert. Das Problem heißt dann entscheidbar,
wenn die zugehörige Menge entscheidbar ist.
Beispiel: Das Primzahlproblem ist entscheidbar. Man wandelt das Problem
in eine Mengendarstellung um, indem man die Menge P aller Primzahlen definiert.
Diese Menge ist entscheidbar, weil es einen Algorithmus gibt, der für
eine beliebige natürliche Zahl n ermittelt, ob n zu P gehört
oder nicht.
Sei
A ein endlicher Akzeptor. Ist L(A) = Ø entscheidbar (sog. Leerheitsproblem
für endl. Akzeptoren)?
Ja, das Leerheitsproblem für endliche Akzeptoren ist entscheidbar.
Sei A ein endlicher Akzeptor. Um festzustellen, ob L(A) = Ø ist,
eliminiert man alle Zustände, welche vom Startzustand aus nicht erreichbar
sind. Enthält der Automat danach noch Endzustände, so ist L(A)
nicht leer.
Wie
beweise ich für zwei Mengen A und B, daß A = B gilt?
Die Mengengleichheit von A und B ist zu beweisen, indem ich sowohl
zeige, daß gilt:
-
A ist Teilmenge von B, sowie
-
B ist Teilmenge von A.
(1) ist erfüllt, wenn ich für jedes beliebige Element a
aus A zeigen kann, daß es in B liegt (und somit für alle Elemente
aus A gilt, daß sie auch in B liegen), und für (2) ist zu zeigen,
daß für jedes beliebige b aus B gilt, daß es auch in A
liegt (somit gilt für alle Elemente aus B, daß sie auch in A
liegen). Wenn diese beiden Bedingungen erfüllt sind, erfüllt
sowohl A das Kriterium, eine Teilmenge von B zu sein, als auch B das Kriterium,
eine Teilmenge von A zu sein, und somit folgt: A = B.
Was ist eine partielle
Funktion?
Als partielle Funktion f: M->K wird eine Funktion bezeichnet, der nicht
für jedes x aus M ein y aus K zugeordnet werden kann. Für diese
x existiert also kein Bild in der Menge K. Als Beispiel kann hier die Tangens-Funktion
herangezogen werden, bei der die Funktion für alle x mit x = 90+k*180
(k aus N) nicht definiert ist, da hier eine Division durch Null
auftritt.
Als Definitionsbereich (auch DOMAIN genannt) einer partiellen Funktion
wird die Menge der x aus M bezeichnet, für die es ein Bild y aus K
gibt (f(x) existiert).
Als Wertebereich (oder RANGE) wird die Menge der y aus K angesehen,
die als Bild von mindestens einem x aus M auftreten (also f(x)=y).
Warum
ist eine Menge von Wörtern, die mit der leeren Menge konkateniert
wird, die leere Menge?
Für die Konkatenation . zweier Mengen A, B gilt: A.B
= {u.v | u aus A und v aus B}.
Wenn man nun eine beliebige Menge A mit der leeren Menge konkateniert,
ergibt dies folgendes: A.Ø = {u.v | u aus
A und v aus Ø}. Da in der leeren Menge jedoch keine Elemente enthalten
sind, existiert kein v, weshalb es keine Wörter u.v gibt,
die in A.Ø liegen.
Ist
entscheidbar, ob die von einem endlichen Automaten akzeptierte Sprache
unendlich ist?
Ja, das ist entscheidbar. Ein Algorithmus eliminiert in A zunächst
alle Zustände, die nicht vom Startzustand erreichbar sind, und alle
Zustände, von denen aus kein terminaler Zustand erreicht werden kann.
Wenn dann in der graphischen Darstellung von A ein Kreis enthalten ist,
so ist die akzeptierte Sprache unendlich.
Was ist eine Grammatik?
Eine Grammatik ist ein Methode zur Erzeugung einer Sprache. Formal
ist eine Grammatik ein Quadrupel G={N,T,P,S} aus einer Menge von Nonterminalen
(Variablen) N, von Terminalsymbolen T, einer Regelmenge P und einem Startsymbol
S. Jede Grammatikregel hat die Form P->Q für irgendeine linke Seite
(Prämisse) und rechte Seite (Conclusion) Q. P muß mindestens
ein Nonterminalsymbol enthalten, Q nicht. Eine solche Regel ist zu verstehen
als Ersetzungsregel. Eine Grammatik erzeugt eine Sprache, sie dient also
der Synthese. Das Gegenstück dazu ist der Automat, der Sprachen erkennt,
er dient der Analyse. Für eine Grammatik im allgemeinen gibt es nur
zwei Einschränkungen: Sie darf nur endlich viele Regeln haben, und
jede Regelprämisse muß mindestens ein Nonterminal enthalten.
Das Wort kann im Lauf der Ableitung beliebig wachsen und wieder schrumpfen.
Wenn man die Form, die die Regeln einer Grammatik annehmen können,
beschränkt, erhält man Grammatiktypen und damit auch Sprachtypen
von verschiedenen Schwierigkeitsgraden.
Gibt
es Grammatiken die sowohl links- als auch rechtslinear ist?
Ja, jede reguläre Grammatik (Typ 3) G=(N,T,P,S), die nur Ableitungsregeln
der Form A->B oder A->b mit A,B aus N und b aus T enthält, ist sowohl
links- als auch rechtslinear. Mit Grammatiken dieser Form können nur
endliche Sprachen beschrieben werden, deren Wörter alle die Länge
<=1 haben.
Wie wird
ein indirekter Beweis durchgeführt?
Bei einem indirekten Beweis nimmt man an, daß die zu beweisende
Behauptung A gerade falsch ist. Man stellt also eine zur eigentlichen Behauptung
A gegenteilige Behauptung ¬A auf.
Nun führt man einen korrekten Beweis bezüglich ¬A. Dieser
führt jedoch schließlich zu einem Widerspruch. Da aber der Beweis
mit korrekten mathematischen Schlußfolgerungen durchgeführt
wurde (im Idealfall), muß demzufolge die Annahme, dass ¬A korrekt
ist, falsch sein. Nun ist ¬A aber gerade das Gegenteil der Behauptung
A. Demzufolge ist A korrekt, womit man A bewiesen hat.
Diese Beweismethode bietet sich bei Thematiken an, welche nur zwei
mögliche, und konträre, Behauptungen ergeben. Ein Beispiel ist
die Anwendung des Pumping-Lemmas auf Sprachen, die nicht in Reg liegen.
Man nimmt an, die Sprachen wären in Reg, wendet dann das unter dieser
Annahme geltende Pumping-Lemma an und erhält schließlich einen
Widerspruch.
Wieviele
endliche deterministische Automaten mit n Zuständen gibt es?
Sei X das Eingabealphabet des Automaten mit |X|=m. Dann gibt es 2n
* nn*m endliche deterministische Akzeptoren. Die Faktoren ergeben
sich durch folgende Überlegung:
-
2n: weil jeder Zustand entweder terminal oder nichtterminal
sein kann,
-
nn*m: weil man von jedem Zustand bei Eingabe jedes Zeichens
in einen der n Zustände wechseln kann.
Was ist
die Backus-Naur-Form?
Die Backus-Naur-Form ist eine Form, die es ermöglicht, kontextfreie
Grammatiken zu verkürzen. Hat man eine kontextfreie Grammatik G=(N,T,P,S)
bei der N die nichtleere, endliche Menge nicht-terminaler Symbole, T die
nichtleere, endliche Menge von Terminalsymbolen, P die nichtleere endliche
Menge an Ableitungsregeln (teilweise auch als Produktionsregeln bezeichnet)
und S aus N das Startsymbol ist.
Beispiel:
T = {a,b}, N = {a}, P = { S->aSb, S->eps}
Diese Grammatik beschreibt die folgende Sprache: L(G)={anbn
| n ³ 0}.
In der Backus-Naur Form werden mehrere Ableitungsregeln zu einer zusammengefasst:
Die Regeln um die Regeln zusammenzufassen sind:
-
A->w1, A->w2, ..., A->wn können zusammengefasst
werden in A->w1|w2|...|wn. Dabei sind
w1,w2,...,wn bel. Wörter aus Nonterminals
und Terminals.
-
A->uv, A->uwv können zusammengefasst werden zu A->u[w]v mit u, v,
w Wörter aus Nonterminals und Terminals.
-
A->uw, A->uBw, B->v, B->Bv mit u, v, w Wörter aus Nonterminals und
Terminals können zusammengefasst werden zu A->u{v}w (0,1 oder mehr
v's)
Beispiel: das Beispiel oben, ist hierfür leider nicht zu gebrauchen,
da es unverändert bleiben würde.
T={a,b,c,d}, N = {A,B,C,D}, P = {S->ABC, A->a, A->c, B->abc, B->ac,
C->bDd, C->bd, D->a, D->Da}
Die beiden A Regeln können zusammengefasst werden: A->a|c
Die beiden B Regeln können zusammengefasst werden: B->a[b]c
Die C und D Regeln können zusammengefasst werden: C->b{a}d
Dann ist P' = {S->ABC, A->a|c, B->a[b]c, C->b{a}d}
Wann
stoppt ein endlicher deterministischer Akzeptor seine Berechnung?
Der Akzeptor beendet seine Berechnung, wenn das Eingabewort vollständig
gelesen wurde. Dann wird nachgesehen, ob er sich in einem Endzustand befindet
und das Eingabewort akzeptiert oder nicht. Durchläuft er vorher bei
der Berechnung Endzustände, so hat das keine Auswirkung.
Enthält
jede unendliche Sprache das leere Wort?
Nein, ein Gegenbeispiel ist z.B. {ab}+={ab}{ab}*.
Ist
jede Teilmenge der Menge X* eine reguläre Sprache?
Nein, innerhalb von X* kann man viele verschiedene Sprachen definieren,
z.B. die Sprachen der verschiedenen Stufen der Chomsky-Hierarchie. Nur
eine kleine Klasse sind die regulären Sprachen.
Ein konkretes Gegenbeispiel: L(G)={anbn | n ³
0} ist nicht regulär und liegt in X* mit X={a,b}.
Wie
lautet (bezüglich der Inklusion) die kleinste und die größte
reguläre Sprache über X?
Die kleinste reguläre Sprache in X* ist die leere Menge und die
größte Sprache ist X* selbst.
Was
ist eine totale Funktion und wie entsteht sie aus einer partiellen Funktion?
Als totale Funktion f: M->K wird eine Funktion bezeichnet, bei der
für alle x aus M ein Bild y aus K definiert ist. Das bedeutet, dass
man für jeden Wert x aus M als Eingabe, eine Ausgabe erhält,
die ein y aus K ist.
Das Umwandeln einer partiellen Funktion f: M->K in eine totale Funktion
g: M->B bezeichnet man als Anreicherung. Hierbei wird für alle diejenigen
x aus M, denen kein Bild y aus K zugewiesen wird, ein Spezialsymbol eingeführt,
welches dann als Bild dieses x aus M gilt. Dieses Spezialsymbol wird häufig
als 'Bottom' bezeichnet. Die totale Funktion g: M->B entsteht also aus
f: M->(K vereinigt mit {Bottom}).
Was besagt der Satz
von Rice?
Der Satz von Rice besagt anschaulich, daß alle nichttrivialen
(nicht einfachen) Eigenschaften von berechenbaren Funktionen und damit
von Algorithmen unentscheidbar sind. Als trivial gelten beispielsweise
Eigenschaften wie, ob der Algorithmus eine bestimmte Länge hat oder
ob er eine bestimmte Zeichenkette enthält. Nichttrivial sind hingegen
Eigenschaften, ob er eine bestimmte Ausgabe erzeugt, ob eine bestimmte
Anweisung ausgeführt wird etc.
Es ist also so, dass nahezu alle interessanten Eigenschaften über
Algorithmen, wie Korrektheit, Terminierung, bestimmtes Verhalten u.ä.
unentscheidbar sind.
Dies wird in dem folgenden Satz beschrieben:
Wenn S eine nicht-triviale Menge berechenbarer Funktionen ist, dann
ist die Sprache L(s) nicht entscheidbar.
Nichttrivial heißt hier: S ist nicht leer und auch nicht identisch
zur Menge der berechenbaren Funktionen.
Was sind Ableitungsbäume?
Um Sprachen zu erzeugen, verwendet man Grammatiken und ihre Produktions-
bzw. Ableitungsregeln. Um den Ableitungsprozeß bei kontextfreien
Grammatiken mithilfe der Produktionsregeln grafisch darzustellen, benutzen
wir Ableitungsbäume.
Jede Ableitung/Ersetzung, jede Erzeugung eines Wortes läßt
sich durch einen Ableitungsbaum beschreiben, in dem die Wege die Ableitungsschritte
widerspiegeln und in dem das erzeugte Terminalwort an den Blättern
von links nach rechts abgelesen werden kann. Zu jedem Ableitungsbaum gehört
genau eine Linksableitung.
Warum
kann die in der Vorlesung vorgestellte abstrakte Maschine alle Funktionen,
auch nicht-berechenbare, in einem Schritt berechnen?
Dieses scheint ein Paradox zu sein, da es - wie bewiesen - unendlich
viele algorithmisch unberechenbare Funktionen gibt, aber jede Maschine
laut Churchscher These einen Algorithmus beschreibt und damit nur eine
berechenbare Funktion beschreibt.
Das scheinbare Paradox ergibt sich aus den Definitionen. Erstens ist
eine abstrakte Maschine keine Turingmaschine wie es die Churchsche These
verlangt (eine abstrakte Maschine hat zum Beispiel unendlich viele innere
Zustände). Spezifisch zu der in der Vorlesung dargestellten abstrakten
Maschine: die Zustandsübertragung wurde definiert als:
Tau: IN x IN ---> IN x IN mit Tau (m,n) = (0, f(n))
Hier verbirgt sich der "Trick": Die Maschine kann einfach in einem Schritt
jede Funktion berechnen, weil es so in der Zustandsübertragung definiert
werden kann. Wie f(n) ermittelt wird, ist nicht beschrieben. Das kann bei
einem endlichen Automaten oder einer anderen realisierbaren Maschine nicht
der Fall sein, weil er sonst eine unendlich große Tabelle bräuchte,
um die Zustandsübertragung auszuführen.
Ist
die Vereinigung zweier linkslinearer Sprachen wieder linkslinear?
Ja. Seien dazu L1 und L2 linkslineare Sprachen. L1 und L2 sind damit
zugleich reguläre Sprachen. Die Klasse der regulären Sprachen
wiederum ist gegen Vereinigung abgeschlossen. Also ist L1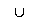 L2
wieder eine reguläre Sprache, für die es eine linkslineare Grammatik
geben muß.
L2
wieder eine reguläre Sprache, für die es eine linkslineare Grammatik
geben muß.
Man kann die linkslineare Grammatik direkt aus den beiden linkslinearen
Grammatiken für L1 bzw. L2 konstruieren. Seien L1=L(G1) mit G1=(N1,T1,P1,S1)
und L2=L(G2) mit G2= (N2,T2,P2,S2), wobei G1 und G2 linkslinear sind. Durch
Umbenennen kann man erreichen, daß N1 und N2 disjunkt sind. S sei
ein Zeichen, das in Vereinigung von N1 und N2 nicht vorkommt. Dann erzeugt
folgende Grammatik G=(N,T,P,S) die gesuchte Sprache L=L1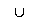 L2
:
L2
:
-
N=N1
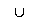 N2
N2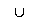 {S}
{S}
-
T=T1
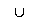 T2
T2
-
P=P1
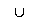 P2
P2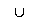 {S->S1,S->S2}
{S->S1,S->S2}
Wenn man aus dem Startsymbol S mit Hilfe der Regel S->S1 das Startsymbol
S1 der Grammatik G1 erzeugt hat, so können alle Wörter aus L1
erzeugt werden.
Wenn man aus dem Startsymbol S mit Hilfe der Regel S->S2 das Startsymbol
S2 der Grammatik G2 erzeugt hat, so können alle Wörter aus L2
erzeugt werden. Daraus folgt, daß L = L1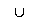 L2
linkslinear ist.
L2
linkslinear ist.
Wie
kann man aus einem nichtdeterministischen endlichen Automaten A einen äquivalenten
deterministischen endlichen Automaten A' mit L(A)=L(A') konstruieren?
Dies kann man mit Hilfe einer Potenzmengenkonstruktion. Da es in A
zu jedem Zustand s und einem gelesenen Zeichen mehrere mögliche Folgezustände
geben kann, konstruiert man jeweils einen Zustand von A' als eine Menge
von Zuständen von A. Zuerst fasst man alle Anfangszustände des
nichtdeterm. endl. Automaten in einer Menge {s01,..,s0N} als neuen Anfangszustand
des determ. endl. Automaten zusammen. Für jeden Buchstaben des Alphabets
muß A' immer einen delta-Übergang haben, wobei von diesem neuen
Anfangszustand aus man die Zustandsübergänge bei Einlesen des
entsprechenden Zeichens des Alphabets für jeden einzelnen Zustand
aus dieser Menge betrachtet. Erfolgt beispielsweise in A von zwei Anfangszuständen
s01 und s02 der Übergang bei Einlesen eines Zeichens a in s01, s02,
s2 und s5, so fasst man diese vier Zustände als Menge {s01, s02, s2,
s5} des Folgezustands für A' zusammen, der durch Einlesen des Zeichens
a vom Anfangszustand {s01, s02} des endl. determ. Automaten A erreicht
wird. Vom neuen Folgezustand aus betrachtet man nun wieder die Zustandsübergänge
für jeden einzelnen Zustand aus dieser neuen Menge, wobei man fertig
ist, wenn man keine neuen Zustandmengen erhält. Terminale Zustände
von A' sind dabei jene Zustandsmengen, die mindestens einen Endzustand
von A enthalten.ÊÊ
Was ist ein Palindrom?
Eine Zeichenkette w, die vorwärts und rückwärts gelesen
dasselbe ergibt. Man sagt auch w=wR, wobei wR die
gespiegelte (engl. reflected image) Version von w bezeichnet.
Beispiel: Palindrome über dem Alphabet {0,1}: epsilon, 0, 1, 00,
11, ..., 011010110, ... Die Menge dieser Palindrome ist eine unendliche
Sprache. Folgende kontextfreie (tatsächlich lineare) Grammatik G=(N,T,P,S)
erzeugt alle Palindrome über {0,1}: N={S}, T={0,1}, P={S->0S0, S->1S1,
S->eps, S->0, S->1}. Die Sprache der Palindrome über {0,1} ist nicht
regulär (warum?).
Die Menge aller Palindrome stellt keine Sprache dar,
da die Zeichenketten nicht aus einem endlichen Alphabet gebildet werden,
wie es die Definition einer formalen Sprache festlegt.
Wie
beschreibt man einen deterministischen endlichen Akzeptor?
Einen endlichen deterministischen Akzeptor A beschreibt man durch ein
5-Tupel A=(X,S,delta,s0,F) mit:
-
X und S sind endliche nichtleere Mengen, X ist das Eingabealphabet, S die
Zustandsmenge
-
delta: S x X -> S ist eine Funktion, die Zustandsüberführungsfunktion
-
s0 ist ein Element von S; s0 ist der Anfangszustand
-
F ist Teilmenge von S, die Endzustandsmenge.
Die Menge L(A)={w Element von X* | delta(s0,w) Element von F} heißt
die akzeptierte (erkannte) Sprache. Eine Sprache heißt endlich akzeptiert,
wenn es einen endlichen deterministischen Akzeptor A gibt mit L(A).
Was ist eine reguläre
Sprache?
Eine Sprache L aus X* (X sei ein beliebiges Alphabet) heißt regulär,
wenn es einen regulären Ausdruck R aus Reg(X) mit sigma(R)=L gibt.
Die Menge aller regulären Sprachen über einem Alphabet X nennt
man R(X). Die Klasse aller
regulären Sprachen bezeichnet man mit R.
(R ist lt. Skript ein deutsches
R)
Was sind Epsilon-Übergänge?
Epsilon-Übergänge in nichtdeterministischen Automanten sind
spontane Zustandswechsel, die ohne das Lesen eines Zeichens stattfinden.
Epsilon-Übergänge können immer geschehen, wenn das leere
Wort eingelesen wird, das beliebig zwischen zwei Zeichen eines Wortes enthalten
sein kann.
Was bedeuten die Begriffe
"Wort", "Alphabet", "Sprache"?
Ein Alphabet X ist eine endliche, nicht leere Menge von Buchstaben.
Ein Wort w über X ist eine endliche Folge von Buchstaben aus X.
Ist diese leer, dann spricht man vom leeren Wort epsilon, welches aus null
Buchstaben besteht.
Eine Sprache L ist jede Teilmenge von X*.
Ist die Definition der Syntax von L gegeben, so spricht man oft von
einer formalen Sprache.
Was besagt die Churchsche
These?
Jede im intuitiven Sinne berechenbare Funktion ist maschinell berechenbar
und umgekehrt.
Wie
bestimme ich zu einer rechtslinearen Grammatik in Normalform einen endlichen
Akzeptor?
Die Zustandsmenge S des Automaten entspricht der Menge der Nonterminalsymbole
N vereinigt mitÊeinem eventuellen zusätzlichen Zustand K, der zugleich
terminal ist.ÊÊÊÊÊÊ
Die Grammatik muß in Normalform sein, d.h.: bei allen Regeln
der Form A->wB oder A->w besteht w nur aus einem Zeichen, und Kettenregeln
dürfen auch nicht vorhanden sein.
-
Der Startzustand des Akzeptors erhält die Bezeichnung des Startsymbols
der Grammatik.
-
Für jede Regel der Form "A->aB" aus der GrammatikÊwird ein Pfeil vom
Zustand A zum Zustand B gezeichnet (B muß eventuell auch erst gezeichnet
werden) und über denÊPfeil wird das a geschrieben.
-
Für jede Regel der Form "A->epsilon" des aktuell betrachteten Zustands
wird Zustand A als terminaler Zustand markiert.
-
Für jede Regel der Form "A->a" des aktuell betrachteten Zustands ist
Zustand K der terminale Folgezustand mit Übergang a.
-
Nun wird eine neue Regel der Grammatik gewählt, mit Schritt 2 fortgefahren,
bis alle Regeln der Grammatik behandelt wurden.
Was ist ein regulärer
Ausdruck?
Reguläre Ausdrücke stellen eine Art dar, Sprachen zu spezifizieren.
An sich sind reguläre Ausdrücke sinnleere Zeichenketten. Erst
durch eine Interpretation erhalten sie eine Bedeutung.
Definition regulärer Ausdrücke:
Sei X ein Alphabet und V ={ (,),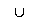 ,
*,., Ø} ein Zeichenvorrat. Die Menge Reg(X) der regulären
Ausdrücke über X ist folgendermaßen definiert.
,
*,., Ø} ein Zeichenvorrat. Die Menge Reg(X) der regulären
Ausdrücke über X ist folgendermaßen definiert.
-
Alle x aus X sind in Reg(X)
-
Ø ist in Reg(X)
-
Für alle R, Q aus Reg(X) gilt: (R
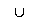 Q)
ist in Reg(X), und (R.Q) ist in Reg(X)
Q)
ist in Reg(X), und (R.Q) ist in Reg(X)
-
Für alle R aus Reg(X) ist R* in Reg(X)
-
Reg(X) ist die kleinste Teilmenge von (X
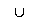 V)*,
die (1)-(5) erfüllt.
V)*,
die (1)-(5) erfüllt.
Wieviele
Zustände hat ein minimaler deterministischer endlicher Automat (DFA)?
Es gilt: |S| = |KL|, wenn S die Menge der Zustände des minimalen
deterministischen endlichen Automaten und KL die Menge der Äquivalenzklassen
ist. Denn bei der Minimierung eines DFA werden äquivalente Zustände
in Äquivalenzklassen zusammengefasst. Diese stellen dann die Zustände
des minimalen DFA dar.
Ist
entscheidbar ob zwei endliche Automaten äquivalent sind, d.h. die
gleiche Sprache akzeptieren (sog. Äquivalenzproblem)?
Ja, das Äquivalenzproblem ist entscheidbar.
Gegeben seien zwei EA, die die Sprachen L1 bzw. L2 akzeptieren. Da
die regulären Sprsachen gegen Komplement abgeschlossen sind, sind
damit auch die Komlemente von L1 und L2 regulär. Der Ausdruck L3=(L1
geschnitten ¬L2) vereingt (¬L1 geschnitten L2) ist ebenfalls regulär.
Daher können wir einen EA angeben, der L3 akzeptiert. L3 ist genau
dann nicht leer, wenn L1 ungleich L2 ist. Es wurde aber bereits gezeigt,
das L3=leer entscheidbar ist. D.h. das Äquivalenzproblem ist entscheidbar.
Wann
heißen eine Grammatik G und eine Sprache L mehrdeutig?
Eine Grammatik G heißt mehrdeutig,
-
g.d.w. es gibt für ein und dasselbe Wort w mindestens zwei verschiedene
Syntaxbäume,
-
g.d.w. es gibt zwei voneinader verschiedene Linksableitungen,
-
g.d.w. es gibt für ein Wort w zwei voneinader verschiedene Rechtsableitungen.
Eine Sprache L heißt mehrdeutig, g.d.w. jede Grammatik G für
L ist mehrdeutig. Man nennt die Sprache auch inhärent mehrdeutig.
Welche
Beschreibungsmöglichkeiten gibt es, um eine reguläre Sprache
zu definieren?
Man kann reguläre Sprachen u.a. definieren durch
-
einen endlichen Akzeptor bzw. Automaten,
-
einen regulären Ausdruck,
-
Angabe endlich vieler Äquivalenzklassen,
-
eine Grammatik aus der Klasse der Chomsky-3-Grammatiken.
Wie
beschreibt man einen nicht-deterministischen endlichen Akzeptor?
Einen endlichen nichtdeterministischen Akzeptor A beschreibt man durch
ein 5-Tupel A=(X,S,delta,S0,F) mit:
-
X und S sind endliche nichtleere Mengen, X ist das Eingabealphabet, S die
Zustandsmenge
-
delta: S x X -> 2S (Überführungsrelation) 2S
ist die Menge aller Teilmengen von S
-
S0 ist Teilmenge von S, Menge der Anfangszustände
-
F ist Teilmenge von S, Menge der Endzustände
Der Akzeptor heißt vollständig, wenn (genau wie beim endl. deterministischen
Automat) von jedem Zustand s mit jeder Eingabe x ein Folgezustand erreicht
wird.
Bei nicht-deterministischen endlichen Akzeptoren mit "Epsilon-Übergängen"
muß man bei der Überführungsfunktion folgendes beachten:
-
delta: S x (X vereinigt {epsilon}) -> 2S ist die Zustandsüberführungsfunktion
vom Akzeptor.
Was ist die Chomsky-Hierarchie?
Im Jahre 1959 teilte Noam Chomsky die Grammatiken in eine Hierarchie
ein, welche vierstufig ist, und den Grammatiken den Typ 0, 1, 2 oder 3
zuordnet. Diese Einteilung wird seitdem verwendet.
Das Kriterium für die Aufteilung ist dabei, wie die Regeln einer
Grammatik der entsprechenden Chomsky-Stufe aussehen dürfen, was also
links und rechts des Ableitungszeichens stehen darf. Es läßt
sich aber auch zeigen, daß mit den verschiedenen Grammatiken tatsächlich
verschiedene Sprachen beschrieben werden können.
Chomsky wies den Grammatiken folgendende Typen zu: Eine Grammatik G=(N,T,P,S)
ist
-
vom Typ 3, wenn sie rechtslinear ist,
-
vom Typ 2, wenn sie kontextfrei ist,
-
vom Typ 1, wenn sie kontextsensitiv ist.
-
vom Typ 0 für alle sonstigen Fälle.
Wann
sind zwei Grammatiken äquivalent?
Zwei Gramatiken G1 und G2 sind äquivalent, wenn die von ihnen
erzeugte Sprache gleich ist, also L(G1)=L(G2) gilt.
Oft kann man mit vollständiger Induktion über die Länge
der Wörter oder auch über die Länge der Ableitungen zeigen,
daß Wörter sowohl von G1 als auch von G2 erzeugt werden können.
Was ist eine
kontextsensitive Grammatik?
Für eine kontextsensitive Grammatik (Chomsky-Typ-1-Grammatik)
gilt die Einschränkung, daß auf der linken Seite der Produktionsregel
ein nichtterminales Symbol existieren muß, welches nur unter Beibehaltung
eines Kontextes, sofern ein solcher vorhanden ist, ersetzt werden darf.
Formal läßt sich die kontextsensitive Grammatik so beschreiben:
G = (T,N,P,S) heißt kontextsensitiv, wenn gilt:
Für alle x->y aus P gibt es ein A aus N und w1,w2,v
aus (T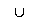 N)*
mit v/=eps, (oder |v|>=1)
N)*
mit v/=eps, (oder |v|>=1)
so daß aus x=w1Aw2 folgt y=w1vw2
Dies bedeutet, daß das Nichtterminalsymbol A nur im Kontext w1...w2
durch v ersetzt werden darf, wenn also w1 und w2
wieder im Wort vorhanden sind. Daher werden diese Grammatiken als kontextsensitiv
bezeichnet
Wann
akzeptiert ein endlicher, nichtdeterministischer, vollständiger Akzeptor
A ein Wort w aus L(A)?
Der nichtdterministische, vollständige Akzeptor akzeptiert ein
Wort w aus L(A), wenn es mindestens einen Weg zu w gibt, der von einem
Anfangszustand in einen Endzustand führt. Beim Einlesen des letzten
Buchstabens von w muß er sich im Endzustand befinden. Daneben darf
es noch viele Sackgassen geben oder Wege, die nicht in einen Endzustand
führen. Wichtig ist aber, das es zu einem Wort w', welches nicht aus
L(A) ist, keinen Weg zu einem Endzustand gibt.
Können
zwei verschiedene Grammatiken die gleiche Sprache erzeugen?
Ja.
Beispiel:
-
erste Grammatik: G1 sei definiert durch G1=({A,B},{b},{A->B,
B->b},A);
-
zweite Grammatik: G2 sei definiert durch G2=({A,B,C},{b},{A->C,
C->B, B->b},A).
Durch vollständige Fallunterscheidung kann man zeigen, dass diese
beiden verschiedenen Grammatiken die gleiche Sprache erzeugen.
Wie
geht man vor, wenn man einen nichtdeterministischen Akzeptor mit Hilfe
einer imperativen Programmiersprache (z.B. C) implementieren möchte?
In der Praxis gibt es nur eine Möglichkeit, dies zu tun, und zwar
indem man den nichtdeterministischen Akzeptor zunächst deterministisch
macht. Dies kann man durch verschiedene relativ einfache Algorithmen erreichen.
Ein deterministischer Akzeptor ist nun leicht zu implementieren, da es
sich im wesentlichen nur um viele if-Abfragen handelt. Denkbar wäre,
dass jeder Zustand eine eigene Funktion darstellen würde, die je nach
Input eine andere aufruft, bis die Eingabe vollständig verarbeitet
ist, dann würde lediglich eine Überprüfung, ob es sich um
einen Endzustand ("Endfunktion") handelt, folgen. Oder man realisiert die
Zustandsübergangsfunktion durch eine Tabelle.
Was ist
die Chomsky-Normalform?
Eine kontextfreie Grammatik G=(N,T,P, )
,wobei
)
,wobei  nicht in L(G) enthalten ist,
heißt dann in Chomsky-Normalform, wenn für alle Regeln a->b
aus P gilt, dass a ein Nonterminalsymbol, also aus N ist, und b entweder
ein Terminalsymbol (aus T) oder aus NN ist (also zwei konkatenierte Nonterminals).
Falls
nicht in L(G) enthalten ist,
heißt dann in Chomsky-Normalform, wenn für alle Regeln a->b
aus P gilt, dass a ein Nonterminalsymbol, also aus N ist, und b entweder
ein Terminalsymbol (aus T) oder aus NN ist (also zwei konkatenierte Nonterminals).
Falls  in L(G) enthalten ist, so
gibt es die Regel
in L(G) enthalten ist, so
gibt es die Regel  ->
-> und
und  kommt in keiner Regel a->b auf
der rechten Seite vor, also b darf nicht
kommt in keiner Regel a->b auf
der rechten Seite vor, also b darf nicht  enthalten. Es gibt zu jeder kontextfreien Grammatik G eine Grammatik G'
in Chomsky -Normalform, so dass L(G)=L(G'). Für reguläre Grammatiken
gibt es auch eine Chomsky-Normalform.
enthalten. Es gibt zu jeder kontextfreien Grammatik G eine Grammatik G'
in Chomsky -Normalform, so dass L(G)=L(G'). Für reguläre Grammatiken
gibt es auch eine Chomsky-Normalform.
Was sind rekursive
Grammatiken?
Um unendlich viele Sätze aus einer Grammatik bilden zu können,
muss in den Regeln der Grammatik mindestens einmal ein Non-Terminal-Symbol
auf der linken Seite (Prämisse) in irgendeiner Regel auf der rechten
Seite (Konklusion) auftreten, wobei auch ein Weg von dem Non-Terminal-Symbol
der Prämisse zum selben Non-Terminal-Symbol der Konklusion existieren
muss. Beispiel: A=> wB, B => Cv, C => wA (indirekt) oder ganz einfach A
=> wA (direkt). In beiden Fällen kann eine Regel mehrfach (rekursiv)
eingesetzt werden. Die in beiden Beispielen genannten Regel können
also beliebig oft angewandt werden, wodurch ein Satz immer mehr Terminal-Symbole
erhält und somit unendlich groß werden kann. Jede Grammatik,
deren Regeln ein beliebig häufiges Wiederanwenden von einer oder mehrerer
Regeln erlaubt, heißt rekursive Grammatik. Unterscheiden kann man
zw. links- (A=>Aw), rechts- (A=>wA) oder zentralrekursiv (A=>vAw). Hinweis:
Bei oben genannten Regeln sind nur Regeln gemeint, bei denen die Wiederanwendung
Terminal-Symbole produziert, nicht z.B. A => B, B => A.
Was
ist ein Automatenmorphismus?
Ein Automatenmorphismus ist eine Abbildung von der Menge der Zustände
eines Automaten in die Menge der Zustände eines anderen Automaten,
so dass beide dieselbe Sprache akzeptieren. Diese Abbildung bildet Startzustand
auf Startzustand sowie Endzustände auf Endzustände ab und erfüllt
für delta die Bedingung, dass es auf das gleiche herausläuft,
ob man vor oder nach einem Übergang die Abbildung ausführt. Das
heißt, ein Automatenmorphismus erhält die Struktur eines Automaten,
die einzelnen Zustände können aber wohl unterschiedlich bezeichnet
werden.
Welche Abschlusseigenschafen
hat DA?
DA ist abgeschlossen gegen Vereinigung, Durchschnitt, Komplement, Differenz,
dass heißt wenn R1, R2 in DA sind, so sind auch R1 vereinigt R2,
R1 geschnitten R2, das Komplement von R1 und R1\R2 in DA.
Was ist das Selbstanwendungproblem?
Beim Selbstanwendungsproblem soll ein Algorithmus entscheiden, ob ein
beliebiger Algorithmus a aus X* terminiert, wenn ihm sein eigener Text
als Eingabe zugeführt wird. Solch ein Algorithmus existiert jedoch
nicht. Somit ist das Selbstanwendungsproblem nicht entscheidbar.
Daher wird das Selbstanwendungproblem als sogenanntes Masterproblem
der Berechenbarkeit bezeichnet. Es wird genutzt, um zu beweisen, das beliebige
andere Probleme, bzw. Funktionen, nicht berechenbar sind, indem man diese,
durch Reduktion, auf das Selbstanwendungsproblem zurückführt.
Welche
Abschlußeigenschaften erfüllt die Klasse der kontextfreien Sprachen?
Kontextfreie Sprachen sind abgeschlossen unter Vereinigung, Produkt
und Sternbildung. Sie sind nicht abgeschlossen unter Schnitt- und Komplementbildung.
Woran
erkennt man eine kontextfreie Grammatik?
Kontextfreie Grammatiken sind so aufgebaut, daß auf der linken
Seite der Ableitungsregeln immer ein Nonterminal steht und auf der rechten
eine beliebige Folge aus Terminals und Nonterminals:
Also gilt: A -> w (w aus (N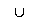 T)*).
T)*).
So läßt sich auch beweisen, ob es sich bei einer beliebigen
Sprache um eine kontextfreie handelt: Wenn man eine Grammatik der oben
genannten Form findet, die die Sprache erzeugt, ist die Sprache kontextfrei.
Was ist das Halteproblem?
Die Frage ist, ob es einen Algorithmus geben kann, der für ein
beliebiges Programm und gegebene Eingabewerte nach endlicher Zeit feststellt,
ob das Programm für diese Werte terminiert oder nicht. Die Antwort
darauf ist nein, es kann keinen solchen Algorithmus geben. Damit in Zusammenhang
stehen auch das Selbstanwendungs- und das Äquivalenzproblem.
Wieso
sind kontextfreie Sprachen nicht abgeschlossen gegen Durchschnittbildung?
Gegenbeispiel: L={anbncm | n,m>=0}
und L'={ambncn | n,m>=0} sind kontextfrei.
Aber ihr Durchschnitt L"={anbncn |
n>=0} ist nicht kontextfrei, was man mit dem Pumping Lemma gut zeigen kann.
Was
sagt das "Wortproblem" aus?
Das Wortproblem ist die Frage, ob es einen Algorithmus gibt, der für
ein beliebiges Wort w und eine beliebige Typ-i-Grammatik G entscheidet,
ob w in L(G) ist oder nicht?
XXX
|
|
Benutzer: gast •
Besitzer: schwill • Zuletzt geändert am:
|
|
|

![]() L2
linkslinear ist.
L2
linkslinear ist.
 )
,wobei
)
,wobei  nicht in L(G) enthalten ist,
heißt dann in Chomsky-Normalform, wenn für alle Regeln a->b
aus P gilt, dass a ein Nonterminalsymbol, also aus N ist, und b entweder
ein Terminalsymbol (aus T) oder aus NN ist (also zwei konkatenierte Nonterminals).
Falls
nicht in L(G) enthalten ist,
heißt dann in Chomsky-Normalform, wenn für alle Regeln a->b
aus P gilt, dass a ein Nonterminalsymbol, also aus N ist, und b entweder
ein Terminalsymbol (aus T) oder aus NN ist (also zwei konkatenierte Nonterminals).
Falls  in L(G) enthalten ist, so
gibt es die Regel
in L(G) enthalten ist, so
gibt es die Regel  ->
-> und
und  kommt in keiner Regel a->b auf
der rechten Seite vor, also b darf nicht
kommt in keiner Regel a->b auf
der rechten Seite vor, also b darf nicht  enthalten. Es gibt zu jeder kontextfreien Grammatik G eine Grammatik G'
in Chomsky -Normalform, so dass L(G)=L(G'). Für reguläre Grammatiken
gibt es auch eine Chomsky-Normalform.
enthalten. Es gibt zu jeder kontextfreien Grammatik G eine Grammatik G'
in Chomsky -Normalform, so dass L(G)=L(G'). Für reguläre Grammatiken
gibt es auch eine Chomsky-Normalform.