|
| |||||||||||
|
Wolfgang Kunz, Johann Wolfgang Goethe-Universität Frankfurt
Hält man Rückschau auf die Entwicklung der Mikroelektronik in den letzten Jahrzehnten, so beeindrucken immer wieder aufs neue die rasanten technologischen Fortschritte für die Herstellung hochintegrierter mikroelektronischer Schaltungen. Der enormen Senkung der Herstellungskosten ist es maßgeblich zu verdanken, daß mikroelektronische Systeme in den vergangenen Jahren Einzug in zahllose industrielle Produkte hielten und aus vielen Bereichen des Alltags kaum noch wegzudenken sind.
Es gibt jedoch eine zweite Entwicklung, die von der Öffentlichkeit
viel weniger beachtet wurde, die aber für den wirtschaftlichen Erfolg
der Mikroelektronik eine genauso entscheidende Rolle gespielt hat wie die
Fortschritte in der Halbleitertechnologie. Gemeint ist die Entwicklung
von rechnergestützten Verfahren zum Entwurf mikroelektronischer
Schaltungen. Die Kostensenkung im Bereich der Fabrikation würde für
den wirtschaftlichen Erfolg eines mikroelektronischen Produktes alleine
nicht ausreichen, wenn nicht auch im Bereich des Entwurfs Maßnahmen
zur Kostensenkung ergriffen würden. Moderne rechnergestützte
Entwurfsmethoden (auch "Computer-Aided Design", CAD) für mikroelektronische
Systeme spielen hier eine zentrale Rolle und nehmen dem Schaltungsdesigner
viele aufwendige Entwurfsarbeiten ganz oder teilweise ab. Hardwareentwurf
mit modernen Entwurfswerkzeugen ähnelt immer stärker dem Softwareentwurf.
Die diesen Werkzeugen zugrundeliegenden Algorithmen sind jedoch ausgesprochen
komplex und nur durch intensive Forschung ist es möglich geworden,
rechnergestützte Verfahren für eine Palette wichtiger Entwurfsaufgaben
zur Verfügung zu stellen. Ein komplettes CAD-System für den Entwurf
mikrolektronischer Systeme kostet in der Regel einen sechsstelligen Dollarbetrag.
Ein implikationsbasiertes Optimierungsverfahren
Die wesentliche Idee eines von uns seit einigen Jahren verfolgten Ansatzes besteht darin, durch Verfahren des deduktiven Schließens verschiedene Algorithmen des rechnergestützten Schaltungsentwurfs zu beschleunigen. Ähnlich wie uns bei einer Autofahrt durch eine unbekannte Stadt Sackgassenschilder vor unerwünschten Wendemanövern bewahren, ermöglicht die Kenntnis über logische Implikationsbeziehungen zwischen den Signalwerten einer Gatternetzliste den Suchraum bei der Lösung von Problemen auf der logischen Ebene des Schaltungsentwurfs einzuschränken. In unserer Arbeitsgruppe sind daher unterschiedliche Kalküle zur automatischen Bestimmung von Implikationsbeziehungen in Schaltungen auf Gatterebene entwickelt und auf verschiedene Problemstellungen angewendet worden. Dies kann relativ leicht am Beispiel eines implikationsbasierten Verfahrens zur Minimierung einer Gatternetzliste nachvollzogen werden, welches im folgenden in vereinfachter Form vorgestellt wird.
Bild 1 zeigt zwei einfache, funktional äquivalente Schaltungen
auf Gatterebene sowie den jeweiligen Booleschen Ausdruck, der durch sie
implementiert wird. Offensichtlich benötigt die rechte Schaltung zur
Implementierung der gleichen Funktion ein Gatter weniger als die linke
Schaltung und würde daher normalerweise bevorzugt. Aufgabe des Optimierungsverfahrens
ist es, die rechte Schaltung aus der linken Schaltung automatisch abzuleiten.
In diesem Fall könnte das auf sehr einfache Weise durch Anwendung
des Distributivgesetzes geschehen, wie anhand der zugehörigen Booleschen
Ausdrücke unmittelbar ersichtlich ist.
|
|
|

|
"schwer berechenbar" |
"leicht berechenbar" |
Bild 1: Ausnutzung logischer Implikationen bei der Schaltungsoptimierung
Sogenannte algebraische Verfahren würden die gezeigte Umformung auch auf diesem Wege durchführen. Man beachte jedoch, daß es im allgemeinen keine leichte Aufgabe ist, durch sukzessive Anwendung der Rechenregeln der Booleschen Algebra eine Schaltung wirksam zu optimieren. Es ist schwer abschätzbar, welche Regeln in welcher Reihenfolge auf welche Bereiche der Schaltung angewendet werden sollen. In unserer Arbeitsgruppe ist daher ein anderer Weg erarbeitet worden, der nicht auf direkter Anwendung der Booleschen Rechenregeln beruht, sondern Schaltungstransformationen aus der Kenntnis von Implikationsbeziehungen ableitet.
Man betrachte das Signal y der linken Schaltung in Bild 1. Der Leser kann sich vergewissern, daß in jeder binären Signalbelegung an den Eingangssignalen a, f und c, die am Signal y den Wert 1 erzeugt, das Signal f den Wert 1 hat, d.h. es gilt y = 1 =>f = 1. Das Bestimmen solcher Implikationsbeziehungen ist leider ebenfalls eine sehr komplexe Aufgabe. Das in unserer Arbeitsgruppe entwickelte Verfahren kann jedoch in realistischen Schaltungen die große Mehrheit der gültigen Implikationsbeziehungen relativ schnell bestimmen.
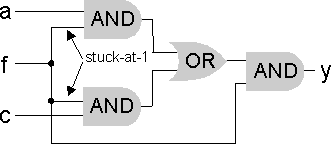
Bild 2: Durch Implikation transformierte Schaltung
Gilt in einer Schaltung für beliebige Signale f und y die Implikationsbeziehung y = 1 =>f = 1, kann man das Signal f über ein UND-Gatter zusätzlich mit y verbinden, ohne die Funktion der Schaltung zu ändern. Aus der linken Schaltung in Bild 1 ergibt sich somit die in Bild 2 gezeigte Schaltung. Ähnliche Umformungsregeln kann man sich leicht für andere Typen von Implikationsbeziehungen überlegen.
Die in Bild 2 zusätzlich eingefügten Schaltungselemente erscheinen zunächst redundant. Werden solche Schaltungselemente jedoch "geschickt" eingefügt, kann das zur Folge haben, daß nicht nur die eingefügten, sondern auch andere Schaltungselemente redundant werden. Um das festzustellen, muß für jedes Signal der Schaltung das sog. stuck-at-Testbarkeitsproblem gelöst werden. Ein Signal ist nicht stuck-at-1- bzw. stuck-at-0-testbar, wenn es durch eine konstante 1 bzw. 0 ersetzt werden kann, ohne die Funktion der Schaltung insgesamt zu verändern. Sonst ist das Signal stuck-at-testbar. In der Schaltung aus Bild 2 sind die mit stuck-at-1 gekennzeichneten Eingänge der beiden vorderen UND-Gatter nicht stuck-at-1-testbar.
Die Überprüfung der stuck-at-Testbarkeit ist NP-vollständig. Alle zur Zeit bekannten Algorithmen benötigen exponentielle Laufzeit. Die dazu eingesetzten Algorithmen können ebenfalls aus der Kenntnis von Implikationsbeziehungen profitieren. Nachdem man mit einem geeigneten Algorithmus für die Schaltung in Bild 2 die Nichttestbarkeit der beiden Gattereingänge nachgewiesen hat, werden sie durch die konstanten Signale ersetzt. Da nach den Booleschen Gesetzen a.1 = aund c.1 = cgilt, bedeutet dies, daß die beiden UND-Gatter sogar ganz entfallen und die beiden Eingangssignale a und c direkt an das ODER-Gatter angeschlossen werden können. Nach dieser Vereinfachung ergibt sich die rechte Schaltung aus Bild 1.
Der beschriebene Transformationsmechanismus (Bestimmung einer Implikation, entsprechende Umformung, Redundanzeliminierung) mutet im Vergleich zur schlichten Anwendung des Distributivgesetzes ausgesprochen kompliziert an, erweist sich aber bei schwierigeren Beispielen als sehr vorteilhaft. Für die Optimierung durch wiederholte Anwendung der Booleschen Rechenregeln ist nämlich kaum eine Heuristik bekannt, die Hinweise gibt, welche der Gesetze in welcher Reihenfolge wo in der Schaltung anzuwenden sind. Auch beim implikationsbasierten Ansatz stehen wir zunächst vor der Schwierigkeit, aus den vielen in der Schaltung existierenden Implikationen gerade diejenigen herauszusuchen, die tatsächlich zu einer Optimierung der Schaltung führen. Glücklicherweise erlaubt die implikationsbasierte Vorgehensweise jedoch den Einsatz einer effektiven Heuristik.
Betrachtet man die linke Schaltung in Bild 5, so ist die Implikationsbeziehung y = 1 => f = 1 nur mit Mühe nachzuvollziehen. Für die rechte Schaltung ist offensichtlich, daß eine 1 am Ausgang des UND-Gatters auch eine 1 an jedem seiner Eingänge und somit auch an f impliziert. Dreht man diesen Zusammenhang um, ergibt sich die von uns verwendete Heuristik für die Schaltungsoptimierung: schwer ableitbare Implikationen zwischen Signalwerten sind ein Symptom schlecht optimierter Schaltlogik und müssen verstärkt zur Durchführung von Transformationen nach dem oben erklärten Schema herangezogen werden.
Es kann nachgewiesen werden [3], daß implikationsbasierte Transformationen den gesamten Booleschen Regelsatz erfassen und prinzipiell jede funktional gültige Schaltungstransformation durchführen können. Mit Hilfe der oben beschriebenen Heuristik in Kombination mit dem implikationsbasierten Transformationsmechanismus ist es gelungen, ein Optimierungsverfahren zu entwickeln, welches nicht nur in Hinblick auf die Optimierungsqualität die auf algebraischen Umformungen basierenden Verfahren übertrifft, sondern in vielen Fällen auch deutlich schneller ist. Inzwischen gelangt dieser Ansatz auch in neueren Versionen kommerzieller CAD-Systeme zum Einsatz. Der beschriebene Ansatz ist ein Beispiel, wie durch geschickte Umformulierung der Problemstellung ein besserer heuristischer Zugang zu einem Problem gefunden werden kann.
Ein weiteres Tätigkeitsfeld unserer Arbeitsgruppe sind die Methoden der formalen Hardwareverifikation. Ziel der formalen Hardwareverifikation ist es, (im Unterschied zur Simulation) mit mathematisch exakten Methoden bestimmte Schaltungseigenschaften zu beweisen. Beispielsweise möchte man beweisen, daß in einem Prozessorkern kein deadlock auftreten kann. Auch in diesem Anwendungsgebiet ist es gelungen, das Problem so aufzubereiten, daß leistungsfähige Verfahren des deduktiven Schließens in Booleschen Netzen eingesetzt werden können, womit erhebliche Fortschritte erzielt worden sind. Allerdings ist man noch weit davon entfernt, ganze Prozessoren formal verifizieren zu können. Es besteht kein Zweifel, daß Erfolg oder Mißerfolg bei der Fortentwicklung der Algorithmen der formalen Verifikation die Produktivität der Mikroelektronikindustrie in künftigen Jahren in hohem Maße beeinflussen wird.
Literatur
| [1] | De Micheli G.: Synthesis and Optimization of Digital Circuits, McGraw-Hill, 1994, ISBN 0-07-016333-2. |
| [2] | Hachtel G., Somenzi F.: Logic Synthesis and Verification Algorithms, Kluwer Academic Publishers, 1996, ISBN 0-7923-9746-0. |
| [3] | Kunz W., Stoffel D.: Reasoning in Boolean Networks, Kluwer Academic Publishers, 1997, ISBN 0-7923-9921-8. |
Adresse
Prof. Dr. Wolfgang Kunz
Professur für Entwurfsmethodik
Fachbereich Informatik
Johann Wolfgang Goethe-Universität
Postfach 11 19 32
60054 Frankfurt/Main
Email: w_kunz@em.informatik.uni-frankfurt.de
WWW: http://em.informatik.uni-frankfurt.de
Lebenslauf
Prof. Dr. Wolfgang Kunz (35 Jahre) ist seit 1998 Inhaber der Professur
für Entwurfsmethodik im Fachbereich Informatik der Universität
Frankfurt. Die Professur, die gegenwärtig drei wissenschaftliche Mitarbeiter
umfaßt, beschäftigt sich mit der Entwurfsautomatisierung für
hochintegrierte Schaltungen.
Herr Kunz hat Elektrotechnik an der Universität Karlsruhe studiert.
Nach seinem Diplom 1989 verbrachte er einen zweijährigen Forschungsaufenthalt
an der University of Massachusetts und promovierte 1992 an der Universität
Hannover in Elektrotechnik. Von 1993-96 war er wissenschaftlicher Mitarbeiter
in der Max-Planck Arbeitsgruppe Fehlertolerantes Rechnen und von 1997-98
am Institut für Informatik der Universität Potsdam, wo er 1996
habilitierte.
Für seine Arbeiten erhielt er den Preis der Berlin-Brandenburgischen
Akademie der Wissenschaften (gestiftet von der Gottlieb Daimler und Karl
Benz-Stiftung), den IEEE Transactions on CAD Best Paper Award und den Gerhard
Hess-Preis der Deutschen Forschungsgemeinschaft.
|